Reliability of Inverse-Synthesis

Technical Issues - Reliability of Inverse-Synthesis

This work was presented at the 2008 SPIE Optical System Design conference in Glasgow and can be downloaded or viewed as follows: printed paper, PowerPoint slides, PowerPoint slides in PDF format (for those who cannot read PowerPoint files).

Addendum June 17, 2014...The work described below has been repeated with ellipsometric targets. Click here for further information and a link to download examples.

Coatings are subject to random, systematic, and gross (operator or machine) errors. In the case of random errors, inverse-synthesis by least-squares fitting provides means to determine which layers had thickness errors. The process is much the same as thin film design, except that here the targets are measured data. But, unlike coating design, where many acceptable solutions are possible, inverse-synthesis requires a unique and correct solution.

We calculate the reliability of inverse-synthesis by the following general method:

Starting with the ideal design, simulate production errors by generating a design with random layer errors. We used relative errors (as in physical thickness monitoring), but absolute errors (as in optical monitoring) can also be utilized.
Calculate the spectrum and convert to optimization targets.
Restore the original design and solve for the randomized design by DLS (damped least-squares) fitting.
If each layer is close to the known original thickness value (i.e. within 0.5%), inverse-synthesis is considered successful, otherwise we have an incorrect solution.

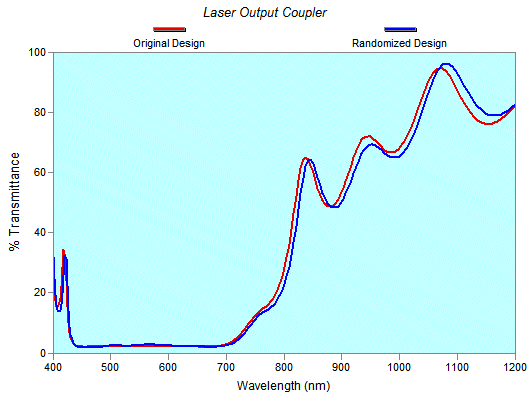
Using FilmStar BASIC, the above sequence is automatically repeated until the statistics become clear, say 50 iterations. The example below shows an iteration of a 26 layer laser output coupler (T=2% from 450-650 nm) with StdDev = 2% random errors.

The same graph zoomed clarifies the deleterious effects of Std Dev = 2% random errors in the range of coating performance.

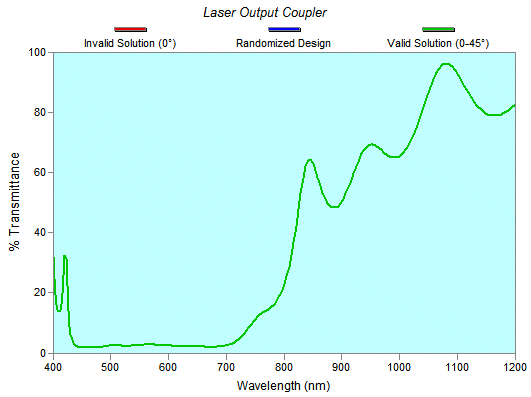
The blue trace (simulating a coating measured at normal incidence from 400 to 1200 nm) is converted to optimization targets and the original (red trace) design restored. Using DLS we solve for the blue spectrum and compare the solution to known layer values. In the case of visible coatings, it seems reasonable to extend measurements to the long wavelength side rather than the short side where dispersion effects will be more pronounced.

The graph below shows results. The blue curve represents the known solution while the red (Invalid Solution, 0°) and green (Valid Solution) curves were calculated by DLS. In the graph below, curves are superimposed and cannot be separated. Most importantly, the graph shows no differences between valid and invalid solutions.

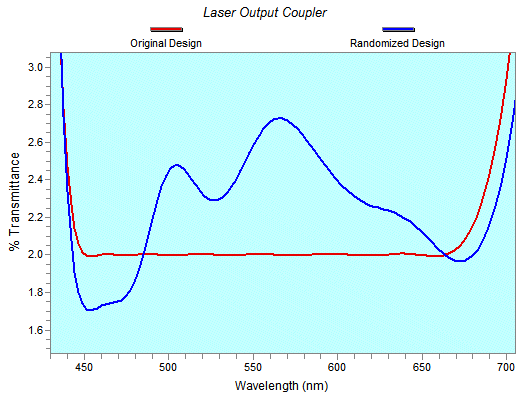
Zooming the graph, we eventually see differences, but notice the %T scale!

Using the range 400-1200 nm and an accuracy criterion of 0.5% we determined that reliability is essentially zero. Adding spectra (targets) at 45° (P & S polarization) increased the reliability to 100%. Our results strongly suggests that coating facilities may achieve dramatic benefits from upgrading their measurement technology well beyond the minimum required for pass/fail analysis. Using the actual performance range 450-650 nm, reliability at either 0° or 0-45° is zero.

Reliability depends on the type of design, number of layers, magnitude of errors, measurement range, angle, and accuracy criterion. Repeating the analysis for a four layer 450-750 nm AR coating with layer StdDev = 5% gave 100% reliability (0.5% accuracy) for calculations over the range 450-750 (0°). When StdDev = 20% (simulating large errors), reliability becomes 56% (0°); expanding the range to 400-1200 nm gives 76% (0°) and 92% (0-45°).

Experienced coating engineers are familiar with these ideas. What is new here is the general method for estimating reliability. While 100% theoretical reliability does not guarantee 100% in practice, failure of the theoretical simulation guarantees failure with measured data.

Suggestions for further work include:

Generate tables showing layer deviations for valid and invalid solutions. Ultimately this will help determine systematic corrections (tooling factor shifts) for optical and physical thickness (crystal) monitors.
Simulate measurement errors (systematic and random) for scanning, diode-array, and FTIR spectrometers. How precise do spectral measurements need to be?
Include refractive index variations.
Perform reliability calculations with ellipsometric quantities in order to compare multiple-angle spectroscopy with multiple-wavelength ellipsometry. Are ellipsometers really necessary? If so, when?

BASIC code (0-45° case) is given below:

Option Explicit
DefInt i-N
DefSng A-H, O-Z
Option Base 1
Public Const Iter = 50      ' change as required

Sub Main
    Dim i, k, IterNG, nLayers, Design0$, qDesign(), qDesc$()
    Dim qSolve(), qType$(), TestPC, bOK As Boolean
    TestPC = Val(InputBox("Enter Verification Level in %", _
             "Reverse Synthesis Test", "0.5"))
    If TestPC > 0 Then
        MainEvents = True   ' enables Abort menu command
        Design0 = Design
        Angle = 0
        For i = 1 To Iter
            AxesDraw
            StatusLabel CStr(i) & "/" & CStr(Iter)
            Design = Design0  ' original design
            CalcRand 0, 1     ' randomize layers, retaining design
            GetLayers nLayers, qDesign(), qType$(), qDesc()
            FileSave "temp.dx"  ' save to replot later
            SpecTargets  True, "R", 1, 0, "R"
            Angle = 45
            Pol = "P"
            Calculate
            SpecTargets False, "R", 1, 45, "P"  ' convert to targets
            Pol = "S"
            Calculate
            SpecTargets False, "R", 1, 45, "S"
            Design = Design0  ' restore original design
            Optimize    ' solve
            GetLayers nLayers, qSolve(), qType$(), qDesc()
            bOK = True
            For k = 1 To nLayers   ' all layers in spec??
                If Abs(qSolve(k) - qDesign(k))/qDesign(k) > TestPC/100 Then
                    IterNG = IterNG + 1 ' fails
                    bOK = False
                    Exit For
                End If
            Next k
            AxesDraw
            LineColor "B"
            FileOpen "temp.dx"
            Replot   ' replot original randomized design
            Wait 2
            If bOK Then LineColor "G" Else LineColor "R"
            Angle = 0
            CalcPlot ' calculate and plot solution at 0°
            Wait 3
        Next i
        Design = Design0
        MsgBox "Confidence Level = " & CStr(100*(Iter- IterNG)/Iter) _ 
                & "%", vbInformation, "Inverse Synthesis 0-45°"
    End If
    LineColor "R"
End Sub

Back to Technical Issues