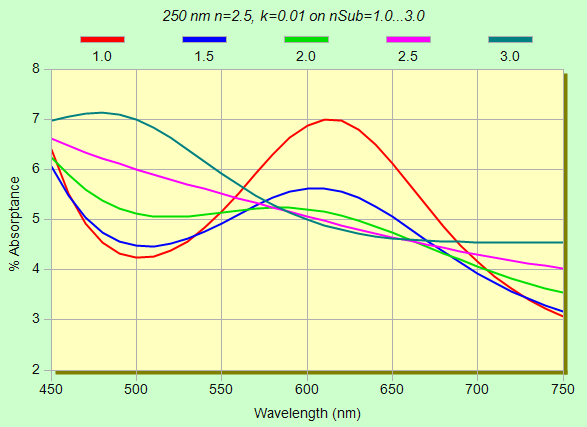
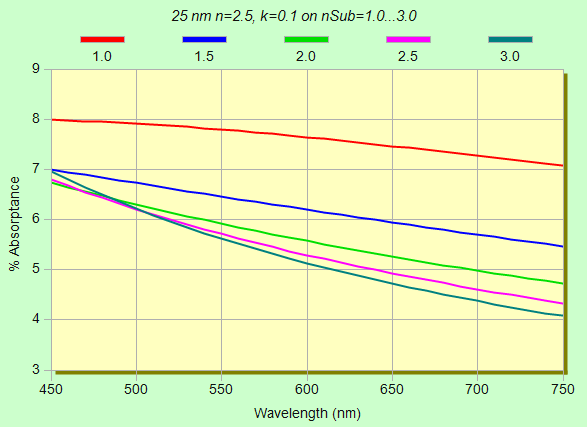
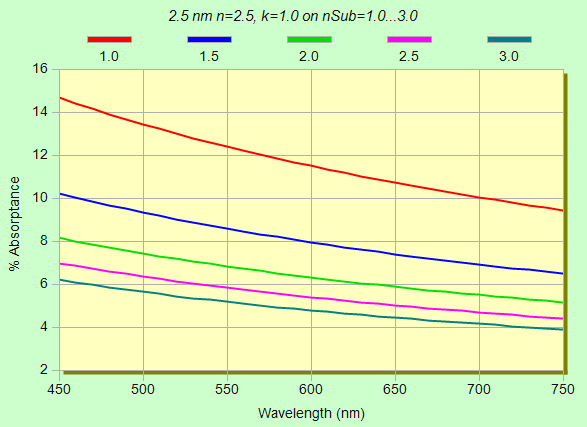
In a LinkedIn discussion  in 2012, a question was raised on how to calculate absorbance of a film-only. Replies did not emphasize that absorption depends on substrate index and film thickness. This is illustrated by the following FilmStar graphs where substrate index is varied from 1.0 to 3.0 for three films: 250 nm (n=2.5, k=0.01), 25 nm (n=2.5, k=0.1), 2.5 nm (n=2.5, k=1.0). Here absorptance is computed as %A=100-%R-%T.

As seen above, when a film is sufficiently thick there are interference effects. Now imagine that the film is within a stack. Obviously layer absorption can change greatly. But as we are only considering a single film, we might guess that the thinner samples shown below are easier to analyze.

A ~1% variation at 450 nm becomes ~8% when k is increased!! Clearly, guesswork is no substitute for the ability to simulate results over the expected ranges of the substrates and films in question.

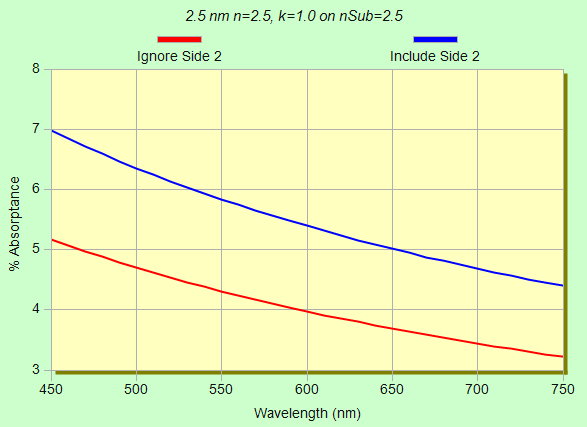
One might assume that the most accurate results for absorption of a film-only are obtained when nFilm matches nSub. But, as shown below, there are also differences if Side 2 (uncoated) reflectance is included. We have exaggerated the effect with a high index substrate. If nSub ~ nFilm ~1.52, these differences will be much less and can probably be ignored.

Why might one think that sample absorbance is independent of substrate index? Possibly because this idea works well in chemistry and spectroscopists as well as instrument service technicians know more about chemistry than thin films. Absorbance is the main quantity of interest for chemists because of its connection with  Beer's Law.

Chemists typically fill a cuvette with solvent and perform a reference scan (aka auto-zero). The material to be studied is then dissolved in the solvent which hardly changes index n. Cuvette and solvent indices are closely matched (~1.48). In this way cuvette absorbance is effectively removed from the sample scan, leaving a sample-only spectrum. Absorbance = -log(Tsample/Tcuvette). A fastidious physicist might argue that this ignores reflectance changes due to sample absorption, but that would only be ~0.2%. Finally, scattering and fluorescence cannot always be ignored.

Note that this is a graph of Absorbance, not % Absorptance.

The pyrex-trichlor-pyrex system was calculated in DESIGN assuming massive layers. In our simulation we implemented auto-zero by subtracting 0.03225 (~92.8%) from computed absorbance values.