Gedankenspektra Ta on BK7

Consider the problem of deducing n,k without a dispersive function like Cauchy or Lorentz. In that case n,k is computed at each wavelength. We have assumed that film thickness is known.

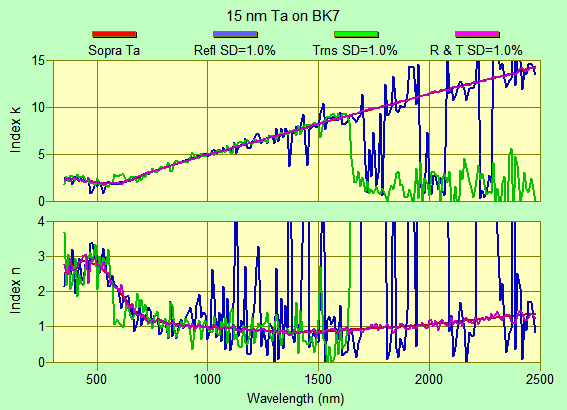
In the plots on this page, n,k solutions are compared with the original Sopra Ta n,k file. A macro computes exact %R/%T then adds random errors (normal  or uniform distribution) and solves via LM optimization using function $NK. Film thickness is fixed. In the plots shown below, the simulation included 0°, 45° P & S and 60° P & S.

We will be working on other strategies. These curves are preliminary and not intended for publication.

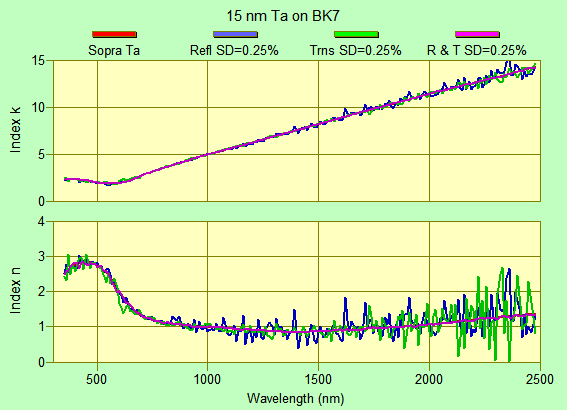
The jump at ~1650 nm is an example of Fred's Anomaly.

The BASIC macro also computes mean error as shown below for the worst SD = 1% case:

15 nm Ta on BK7 Uniform error dist Err = 1%
R only
Mean n error = 1.58E-1 Mean k error = 9.05E-2
Mean n error = 4.98E-1 Mean k error = 3.29E-1
Mean n error = 5.01E-1 Mean k error = 3.69E-1
Mean n error = 3.56E-1 Mean k error = 2.56E-1
Mean n error = 2.42E-1 Mean k error = 1.40E-1

T only
Mean n error = 5.13E-2 Mean k error = 2.72E-2
Mean n error = 4.63E-2 Mean k error = 2.70E-2
Mean n error = 4.86E-2 Mean k error = 2.63E-2
Mean n error = 5.28E-1 Mean k error = 4.67E-1
Mean n error = 5.62E-2 Mean k error = 3.21E-2

R & T
Mean n error = 4.55E-3 Mean k error = 3.69E-3
Mean n error = 4.14E-3 Mean k error = 3.49E-3
Mean n error = 5.13E-3 Mean k error = 3.94E-3
Mean n error = 4.19E-3 Mean k error = 3.45E-3
Mean n error = 4.34E-3 Mean k error = 3.54E-3

When error=0 solutions essentially overlap the Sopra Ta curve, although R + T is still superior:

15 nm Ta on BK7 Err = 0%
R only
Mean n error = 1.85E-5 Mean k error = 2.12E-5

T only
Mean n error = 2.61E-5 Mean k error = 1.44E-5

R & T
Mean n error = 2.20E-6 Mean k error = 1.97E-6